«Математика изобилует яркими идеями. Независимо оттого, как долго и сколь упорно занимаешься математикой, кажется, что никогда не иссякнут в ней удивительные сюрпризы. И никоим образом нельзя считать, что эти сюрпризы можно встретить лишь в трудных задачах, рассчитанных на подготовленных учащихся. Использование всех видов простых понятий требует выдумки и изобретательности. В этой книге обсуждаются десятки элементарных задач, которые были выбраны из публикаций журнала "American Mathematical Monthly" за период 1894-1975 гг. В них содержится множество изумительных идей, а двадцать из них просто прекрасны.

$Описание: C:\Projects\_math\_hmm\Project_Honsberger_Ex16\Pictures\Oblojka_Book1.jpg$

Это не сборник задач, предлагаемых для решения (хотя вы, несомненно, получите больше удовольствия, если прежде, чем прочесть решение, сами подумаете над задачей), а витрина маленьких математических чудес.

Около 100 новелл, в каждой из которых излагается красивая математическая задача. Серьезные математические методы даны в легкой, запоминающейся форме, что способствует воспитанию интереса к математике.»

Материал книги предназначен для школьников старших классов, преподавателей, студентов и всех, кто интересуется математическими задачами.

В конце книги приведены проблемы для самостоятельного изучения.

Нас заинтересовала проблема (задача) №16:

Найдите два натуральных числа таких, что их сумма будет делителем их произведения.

Компьютерное моделирование

К решению проблемы мы подступили с помощью хромоматематических методов.

Была создана программа на языке Delphi. В которой с помощью хромоматематических методов моделировалось решение проблемы Хонсбергера. Моделирование использовалось для визуального обнаружения «скрытых» закономерностей в решениях.

Пример работы программы:

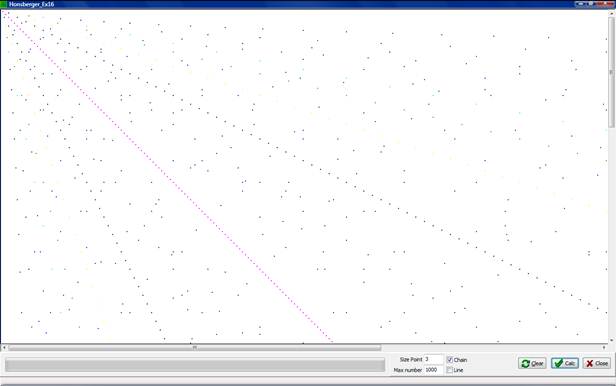
Видны характерные линейные структуры в решениях задачи. Это позволяет высказать предположения о «характере» решений.

Хромоматематическая модель

В программе мы использовали различные хромоматематические модели.

Пример одной из моделей:

Для пар чисел а и b найдем k – результат целочисленного деления а на b. Для одинаковых k будем использовать одинаковый цвет.

Например:

k=1 цвет = Fuchsia;

k=2 цвет = Red;

k=3 цвет = Yellow;

k=4 цвет = Olive;

k=5 цвет = Aqua;

k=6 цвет = Cream;

k=7 цвет = Blue;

k=8 цвет = Silver;

k=9 цвет = Navy;

k=10 цвет = Green;

В результате получим:

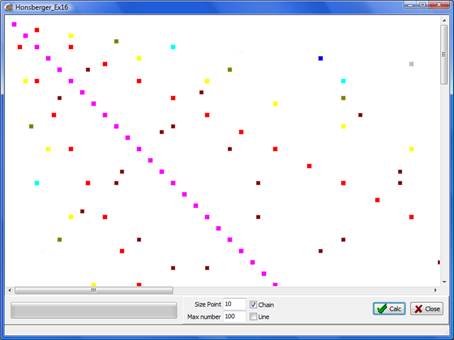
Полученное изображение подсказало нам следующие теоремы:

Теорема о нечетности

Теорема. Если (a; b) – решение, то числа a и b не могут одновременно быть нечетными.

Доказательство.

Поскольку (a; b) – решение, то выполняется равенство:

Допустим, что a и b – нечетные, т.е. a=(2k+1) и b=(2m+1), .

Тогда имеем

(2k+1)(2m+1) = n((2k+1)+(2m+1)) = 2n(k+m+1).

Число (2k+1)(2m+1) – нечетное, а число 2n(k+m+1) – четное. Получили противоречие.

Теорема доказана.

Теорема о диагонали четных чисел

Теорема. Если число a – четное, то (a; a) – решение.

Доказательство.

Если (a; a) – решение, то выполняется равенство:

Пусть а = 2k. Имеем:

Теорема доказана.

Теорема о цепочке

Теорема. Если (a; b) – решение, то и (аk; bk) тоже решение, при .

Доказательство.

Поскольку (a; b) – решение, то выполняется равенство:

Рассмотрим пару (аk; bk)

Положив , получим верное равенство.

Теорема доказана.

Теорема о множителе

Теорема. Для , пара (a; ka) – решение, если а - четное и делится на (k+1).

Доказательство.

При к=1, по теореме о четности (a; а) – решение. Т.е. выполняется равенство:

, т.е.

Рассмотрим пару (a; ka).

По условию а делится на (k+1), а значит, и делится на (k+1), т.е. .

Теорема доказана.

Замечание. Совершенно аналогично рассматривается случай для пары(ka; a).

Заметим, что если мы использовать покрытие «Методом линий», то увидим:

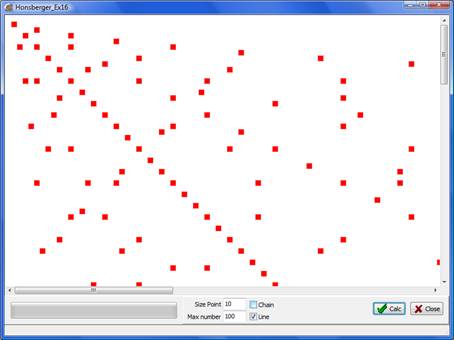
Т.е. покрыты все решения.

Полученные теоремы позволяют сформулировать основную теорему:

Теорема о поиске

1. Для любого натурального a рассмотрим все его делители {n}

2. Для любого делителя n рассматриваем все m, что (n, m) = 1

3. Если (n + m) – делитель a, то b = m/n·a

4. Пара (a, b) – решение проблемы Хонсбергера

Доказательство.

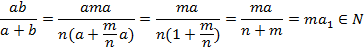
Теорема доказана.

Пример использования теоремы о поиске

Рассмотрим пример работы теоремы для a = 28.

Найдем все D(a) = {1, 2, 4, 7, 14, 28}.

n=28 нас не устраивает, т.к. мы не сможем найти такое m, которое в сумме с n являлось бы делителем a, т.е. 28. Значит, n ≠ 28.

Аналогично получаем, что , n ≠ 14 и n ≠ 7.

n = 4. Найдем все m, чтобы (n,m) = 1. Получим m = 3. Тогда b = ¾·28 = 21.

n = 2. Аналогично получаем m = 5, т.е. b = 70.

n = 1. Получаем m = 1, 3, 6, 13, 27 и соответственно b = 28, 84, 168, 364, 756.

Пары (28, 21), (28, 70), (28, 28), (28, 84), (28, 168), (28, 364), (28, 756) – решения проблемы Хонсбергера.

Обобщенная проблема Хонсбергера

Сформулируем обобщение проблемы Хонсбергера.

А именно:

Найти такие n чисел (a₁,a₂,a₃,…,a_n), произведение которых делится на их сумму.

Рассмотренные ранее теоремы позволяют высказать ряд утверждений для решения обобщенной проблемы Хонсбергера.

Теорема об n одинаковых числах

Теорема. Если число a кратно n, то n чисел (a,a,…,a) являются решением обобщенной проблемы Хонсбергера.

Доказательство.

Имеем:

Теорема доказана.

Пример использования теоремы об n одинаковых числах

Пусть:

n = 3, a = 3·m

В частности:

Теорема о диагонали

Теорема. Для любого с, тройка целых чисел (c + d, d, c) и ей «симметричные» - решения проблемы Хонсбергера. Где для четного с, d любое, для нечетного с, d - четное.

Доказательство. (c + d)dc = k(c + d + d + c)

(c + d)dc = 2k(c + d)

dc = 2k

Теорема доказана.

Результаты работы

· Создана программа на языке Delphi для наглядности заполнения плоскости числами, подходящими для решения.

· Показан хромоматематический подход к решению задачи Хонсбергера.

· Доказана теорема о диагонали четных чисел.

· Доказана теорема о нечетности.

· Доказана теорема о множителе.

· Доказана теорема о цепочке.

· Доказана теорема о поиске.

· Предложено обобщение проблемы Хонсбергера.

· Доказана теорема об n одинаковых числах.

· Доказана теорема о диагонали.

Литература и программные средства

1. Хонсбергер, Росс. Математические изюминки / Росс Хонсбергер ; Пер. с англ.: А.Савин и Л. Савина . - М. : ТЕРРА - Книжный клуб, 2008. - 253 с. : ил. - (Мир вокруг нас). - Пер. изд.: Mathematical morsels/ Ross Honsberger.- ISBN 978-5-275-01736-6

2. Грэхем Р., Кнут Д., Паташник О. Конкретная математика, Мир: М.- 1998

3. Цвырко С. Хромоматематика. Теоремы для суммы, произведения и суммы квадратов. /сб. работ IX городской научно-практической конференции «Шаг в будущее», 2007

4. Система программирования (с) Embarcadero RAD Studio Delphi 2010

5. (с) Microsoft Excel 2007

6. (с) Microsoft Word 2007

7. (с) Microsoft Power Point 2007

8. (с) CorelDRAW X4

Приложения

Листинг программы (фрагмент)

Поскольку листинг программы очень большой, то приведен фрагмент одного из модулей:

procedure TFormHonsberger_Ex16.Draw;

begin

Image1.Canvas.Brush.Color := clBlack;

Image1.Canvas.Rectangle(0, 0, Image1.Picture.Width, Image1.Picture.Height);

SizePoint := StrToInt(LabeledEdit1.text);

MaxA := StrToInt(LabeledEdit2.text);

ProgressBar1.Max := MaxA;

MaxB := MaxA;

b:=1;

y:=0;

repeat

x :=(b-1)*SizePoint;

a:=b;

repeat

if (a * b) mod (a + b) = 0 then begin

Image1.Canvas.Brush.Color := clWhite;

Image1.Canvas.Pen.Color := clWhite;

end

else begin

Image1.Canvas.Brush.Color := clBlack;

Image1.Canvas.Pen.Color := clBlack;

end;

Image1.Canvas.Rectangle(X, Y, X + SizePoint, Y + SizePoint);

Image1.Canvas.Rectangle(y, x, y + SizePoint, x + SizePoint);

x := x + SizePoint;

a := a + 1;

until a > MaxA;

y := y + SizePoint;

b := b + 1;

ProgressBar1.Position := b;

until b > MaxB;

ProgressBar1.Position := 0;

end;